Procedurally Generating Voxel Worlds using Wave Function Collapse
Hello everyone,
I recently introduced my voxel playground, a ray-traced voxel engine made with cellular automata in mind. However, so far the voxel map itself is quite barren. So I set out to populate the world in interesting ways. For a previous project, I had used Wave Function Collapse, and I thought it would be fun to try to apply it to full 3D world generation.
I have implemented two distinct versions of the algorithm. First, a simple tile-based approach that uses premade voxel tiles which are fitted together like jigsaws. The second pattern-based approach is more complicated. It aims to generate an output world that looks similar to the input voxel data.
But first, what is Wave Function Collapse? The algorithm’s name is borrowed from quantum mechanics, but here it simply means we start with a grid of nodes in superposition, meaning each can be in any one of several possible states. We pick one node, collapse it to a specific state, and then apply that state’s connection rules to its neighbors. For example, tiles may only connect if their touching sides match. This process repeats, propagating constraints outward, until ideally the whole grid is collapsed in a way that satisfies all local rules.
Tile-Based Wave Function Collapse
So let’s put this into practice by trying to generate a castle using premade tiles. This gives us a maze of walls, with some magenta cubes in between. These cubes are debug visualizations that represent contradictions. Sometimes, multiple neighbors collapse around a node, with rules that contradict. Once this happens, it implies that no state exists to satisfy all constraints put onto the node. Having even a single contradiction can completely spoil the final result, but luckily there are ways to combat it.

Arguably the easiest way is to add more states that can satisfy the constraints. For instance, by adding a tower state that only has one connection to a wall, we can remove some contradictions. Another way is to duplicate states with rotated an flipped variants. This gives the algorithm way more options.
On the algorithm side, we change the order in which we collapse our nodes. In information theory, there is the idea of Shannon-entropy. The lower the entropy, the more predictable the outcome of a distribution. It is computed as the negative sum of each probability multiplied by its logarithm. At each step in the algorithm, we can compute the entropy for each node in superposition, and collapse the ones with minimal entropy first. Intuitively, we look at the nodes with the least options first, as that reduces the chances of another rule from a neighbor forming a contradiction later. As entropy can change a lot, and we have a lot of nodes, we use a priority queue to efficiently keep track of the nodes in order of increasing entropy.
With this in place, we start generating some more consistent structures, though in this case there is still a problem. We do not expect to generate walls that are cut off by the map boundary. We also want one castle, but now we populate the entire grid with wall pieces. The first issue is solved quite easily. We filter out edge nodes that do not have an outward-facing air side.
The second issue requires some more careful thought. What the algorithm is doing, is perfectly legal with the rules we have laid out. It ensures that neighboring nodes share the same data at their connecting sides, making their connection look reasonable. But when generating structures like a castle, we ideally want one connected structure. In this case, we can add another heuristic to the algorithm. Nodes in superposition now indicate if they have had a rule applied coming from a connection with at least one solid voxel. If so, we allow it to collapse, otherwise we do not.
This system works reasonably well now, although more states or heuristics could be added to improve variety, or systems could be put in place to make the structure blend with the environment better.
Pattern-Based Wave Function Collapse
While the tile-based approach is fairly effective, it does not generate worlds with granularity I had in mind, since everything is strictly aligned to the tile grid. Instead, I wanted to try a pattern-based approach like in the original Wave Function Collapse implementation. The idea is to take an input set, and extract small patterns from it. We then generate an output using only those patterns, appearing at roughly the same rate as they do in the original dataset.

An input voxel model

An example output
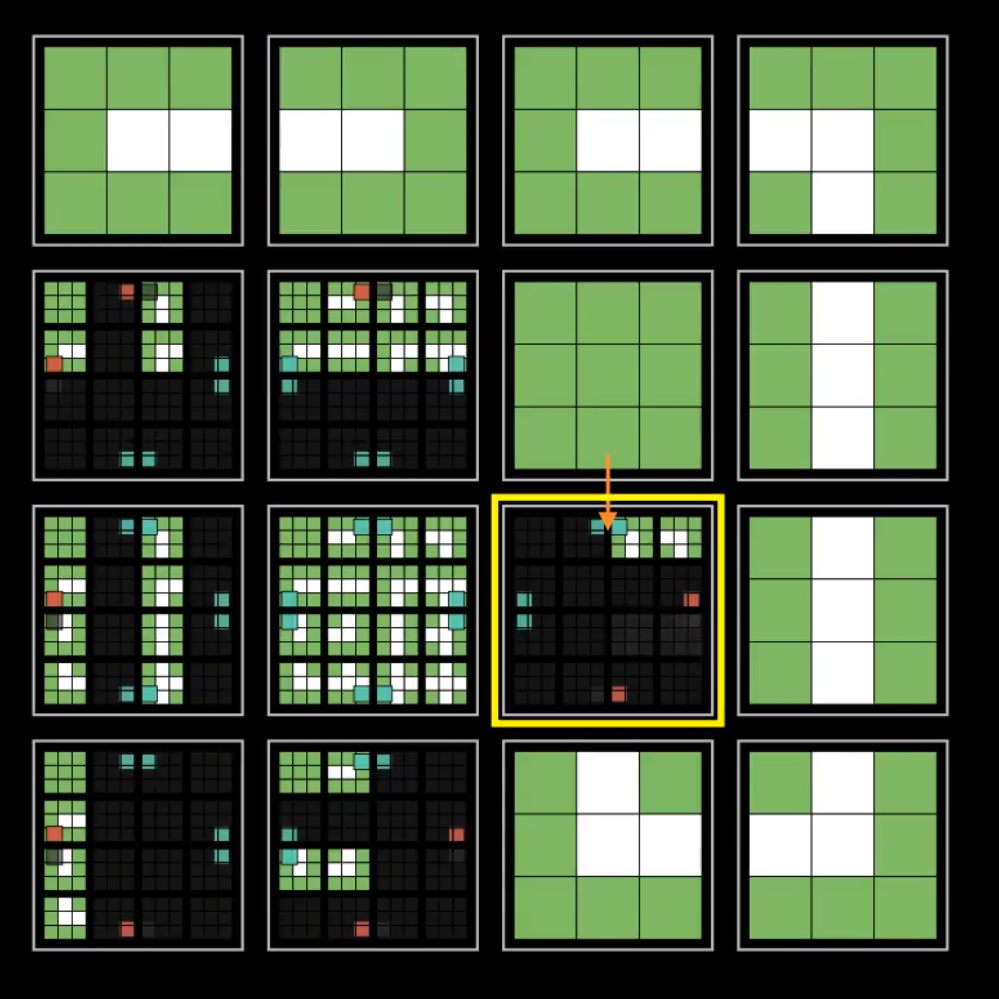
To implement this, we use the same idea as before: a grid of superposition cells that we collapse. However, this time each state is not a particular tile, it is instead a pattern that overlaps with neighboring nodes. We define a neighborhood as either the Von Neumann or Moore neighborhood of a particular radius. We need to keep this radius low, as the cost of the algorithm explodes the larger the neighborhood is. However, larger neighborhoods would be better at replicating larger details from the original data. We extract patterns by sliding a neighborhood-shaped window over the input data set, and counting the number of occurrences of each unique one. These occurrences are then normalized to be used as the prior probabilities for each pattern.

Unique patterns extracted from the input
The way patterns overlap is exactly the way we constrain the system. When a node collapses into a pattern, we disallow all patterns in its neighbors that cannot overlap with it. Importantly, we compute a set of differences between neighborhood offsets, which I refer to as deltas. Essentially, the deltas set consists of all pairwise differences between neighborhood offsets. This gives us the relative position of all nodes whose neighborhood intersects the neighborhood of the currently considered node. These nodes should all be constrained when a node collapses.
In 3D, a Moore neighborhood of radius one contains 27 nodes. The deltas set encompasses a 5x5x5 area, meaning that we have to consider up to 124 neighbors every time a voxel collapses. Therefore, recomputing compatibility every time will be quite costly. Instead, we precompute and store compatibility in 124 P by P matrices, where P is the number of unique patterns, and each entry is a boolean. In C++, we store this as a vector of unsigned integers to both pack these booleans as tightly as possible, and to use binary operations to speed up our program. Each cell in superposition stores a single binary vector of length P to keep track of allowed patterns for the same reasons.
However, when dealing with more complex input patterns, we have a glaring issue. If we only ensure rules are enforced locally, we may run into issues where the algorithm enters an impossible global state. For instance, a tree may be generated in the air, instead of on the ground, and it later causes contradictions by trying to generate grass mid-air itself. This is because the algorithm lacks an understanding of a tree, or any other structure larger than the chosen neighborhood size.

To solve this, we propagate constraints beyond immediate neighbors. Now, when a superposition node loses possible states, we update adjacent nodes so their remaining states are compatible. This restriction can cascade. Each newly limited node may in turn constrain its own neighbors. In practice, we union the bitmasks of all valid states in a given direction, then intersect that with the bitmask of the neighbor in that direction. This is essentially the arc consistency approach from constraint satisfaction problems, as in the AC‑3 algorithm, though our implementation is not particularly efficient.
While this greatly reduces contradictions, it increases runtime, and its benefits may diminish as the number of patterns or output size grows.
Discussion
The wonderful thing about Wave Function Collapse is that we can manually create a world state, and initialize the algorithm with it. In my implementation, we treat all the air voxels as uncollapsed, and determine the pattern for each voxel by sampling from a probability mass function based on the priors of each possible pattern at that position. Furthermore, Wave Function Collapse theoretically works on any input data, though some patterns or tilesets are more prone to contradictions than others, and the quality of them can greatly affect the effectiveness of the algorithm.
Unfortunately, the algorithm is not quite perfect, as even tiny worlds can take quite a while to generate. Compared to classic approaches such as using fractal noise to generate a terrain heightmap, or random walks to generate mazes, Wave Function Collapse can be several orders of magnitude slower. It also cannot be trivially parallelized. If you start solving contradictions using backtracking, its performance might tank even more. Luckily, there are still many ways to improve it. Hierarchical approaches, or seeding the algorithm using other techniques could still make it viable.

Overall, I do think this was a successful experiment, and it is a fun approach to generate many kinds of virtual worlds without having to program new logic. As always, I have published the code under the MIT license, as part of my voxel playgrounds repository.