Training Evolutionary Agents
Last time, I showcased some basics of Evolutionary Algorithms, which can elegantly solve black box problems. Today I extend it to train agents using reinforcement learning and neural networks. If you want to check it out for yourself, feel free to look at the source code.
Reinforcement learning is a branch of machine learning where agents aim to learn some behavior that maximizes the reward obtained in some environment by taking the right actions given a particular state. While many ways and options exist, today I will focus on a rather simplified method, infused with evolutionary algorithms.
Setup
Our goal is to essentially create a brain for an agent. This brain will be nothing more than a function that takes in a vector representing the state the agent is in, and the output indicates the action it should take. For instance, the agent may know its position, and may output a direction to move into next. In our case we represent this brain that processes the input state vector into an action output vector using a neural network.

A simple feedforward neural network is nothing more than a function that transforms a vector into another vector. It does this by moving the input through several layers, where each layer is fully connected to the next one. It’s extremely powerful, as we can approximate many functions by finding the right set or parameters. These parameters are referred to as weights and biases, essentially varying how strong connections are within the network. As these only scale and offset values at nodes in the network, we need some non-linear activation function at each node to enable approximating a wider set of functions, which most commonly seems to be ReLu nowadays.
Evolution
While this idea is rather straightforward, it leaves the challenge of finding the right parameters. Last time, I discussed how Evolutionary Algorithms. only require a fitness evaluation per individual to search for an optimal solution. Thus, we can train our networks by creating a population of valid neural network configurations. For a particular amount of layers and connections, we can compute the required amount of weights and biases. Those concatenated together form one large string of floats, which will be the genome of each individual.
Then, to calculate fitness, we use a simulation. For each individual, we initialize an agent with a neural network using the individual’s genome. We then let the simulation play out, and hand out rewards depending on what happens to the agent. I refer to the accumulated reward at the end of the simulation as the agent’s fitness. Now that we have gathered fitness values for each genome, we can evolve the population, and repeat.
Example: Finding Reward
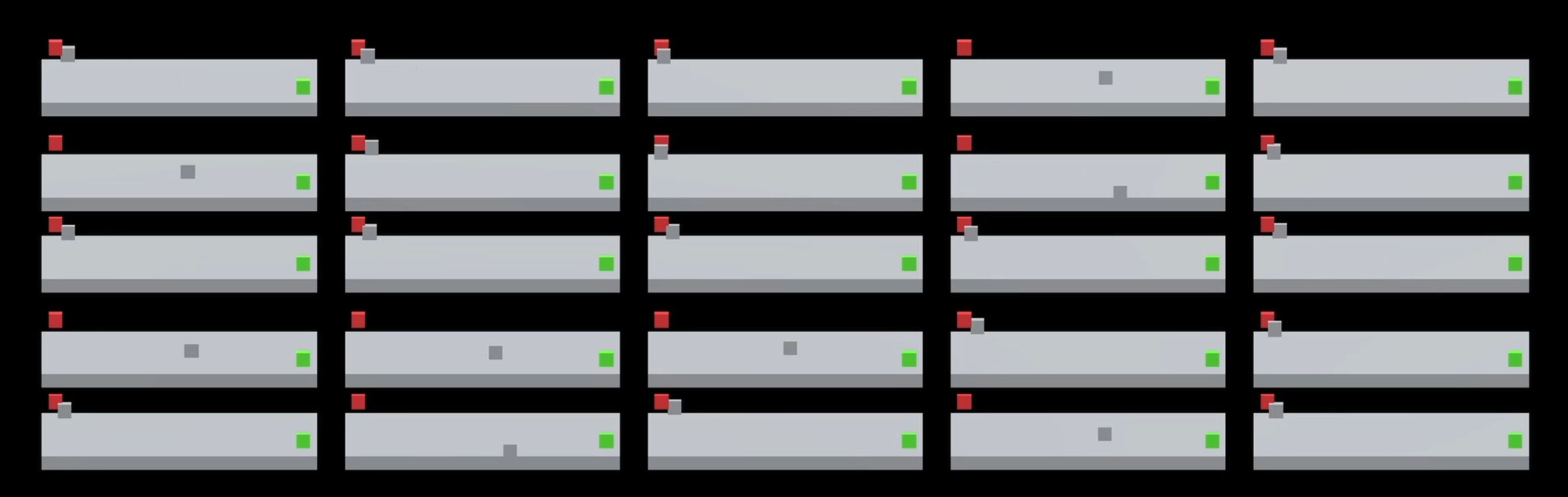
Then, we set up the reward system. First, every tick it gets a penalty of -0.1, as we want it to walk to the goal as fast as possible. The red target acts as a trap of sorts, and gives a small reward of 5. Finally, the green target gives a large reward of 50. This structure should incentivize the agent to walk to the green reward as fast as possible.
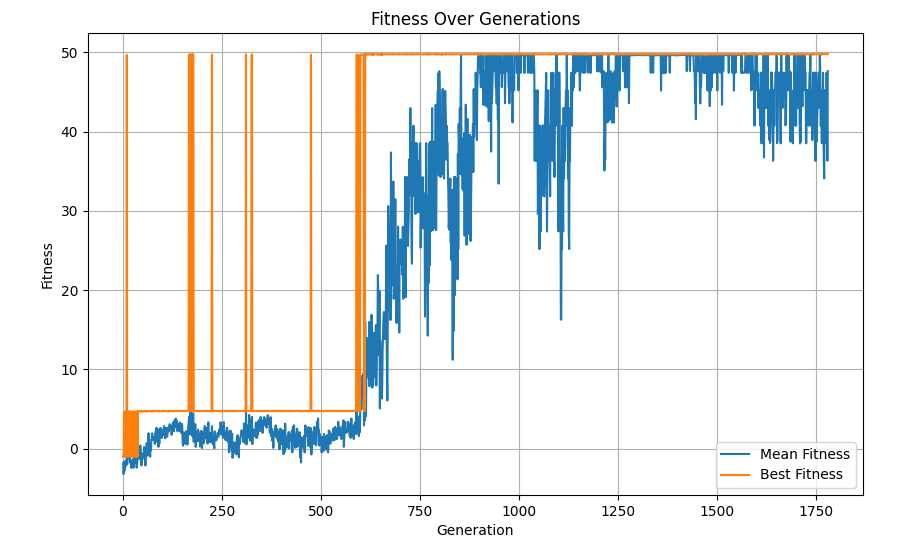
Notice how it falls for the red trap first, but discovers the green better reward next.
Example: Car Racing

As our goal is to train agents to drive without crashing, we reward it for driving longer distances. We do this by evenly spacing reward checkpoints along the track. When an agent collides with one, its reward increases by one. When it collides with the wall, it is punished by deducting 5 reward points. This is on top of the opportunity loss of not being able to collect more rewards that round, as it crashed and cannot move anymore. Therefore, the car is incentivized to drive for as long as possible without hitting the walls. The steering angle is too shallow for it to constantly rotate in place without hitting the walls, so I do not foresee that as a possible exploitation of the fitness function.
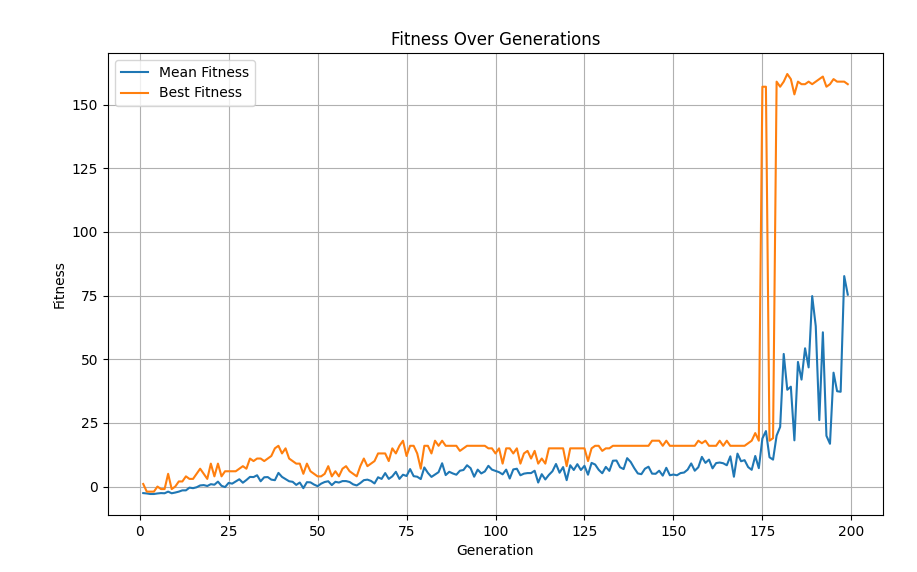
At around 175 generations, it learned to drive the track. Time is cut at 3 minutes in simulation time, so that's why it spikes to ~150 fitness.
Conclusion
While often some form of gradient descent and backwards propagation is used to train neural networks, I wanted to show that EAs can provide a possible alternative. They have some wonderful benefits, such as being insanely parallelizable, and they are more resistant to noise. Even in combination with other techniques, we can use EAs to vary hyperparameters such as network size and learning rate, to come to an optimal neural network faster.
I have made all relevant code open source, and usable as a godot GDExtension. I do not believe it is fully production ready, but I hope it can still be of some use regardless.